Topological Order Intrinsic to Mixed Quantum States
Nature showcases an extraordinary diversity of phases of matter, including many that can be understood only through the principles of quantum mechanics. Such quantum phases can exhibit topological order, characterized by long-range quantum correlations and exotic quasiparticle excitations. Despite extensive theoretical and experimental exploration over the past few decades, our knowledge of topological order has been largely restricted to closed quantum systems. However, real-world quantum systems are inevitably influenced by dissipation and decoherence, underscoring the need for a deeper understanding of open quantum systems—those that exchange energy, particles, or information with their surroundings. Now three research teams have identified new forms of topological order intrinsic to open quantum systems, expanding the spectrum of possible quantum phases and paving the way for advances in quantum information science [1–3].
Conventionally, different phases of matter are classified based on symmetry. For example, ferromagnets break rotational symmetry since their magnetic moments align in a specific direction, even though the underlying physical laws remain invariant under spatial rotation. While this concept of spontaneous symmetry breaking has proven valuable, the past few decades have seen a new paradigm: topological phases of matter. Representative examples of these phases, such as fractional quantum Hall fluids and quantum spin liquids, display topological order [4]. This property does not arise from spontaneous symmetry breaking but from an intricate pattern of entanglement—nonlocal correlations central to quantum physics.
The long-range entanglement of topological order is associated with multiple ground states and quasiparticle excitations known as anyons. The statistical properties of anyons are distinct from those of elementary particles categorized as bosons and fermions, letting these exotic excitations be potential candidates for fault-tolerant quantum computation [5, 6]. Despite the difficulty in experimentally implementing topological order due to its highly entangled nature, researchers have recently observed it on quantum processors made from arrays of quantum bits [7].
However, the existing theoretical framework of topological order has been mainly confined to closed quantum systems isolated from their external environment. The stability of topological order against dissipation and decoherence has yet to be fully evaluated, posing a major challenge for quantum information science and technology, which demand meticulous control and correction of various errors. A fundamental distinction between closed and open quantum systems lies in their quantum states: Whereas closed systems exhibit pure states described by single wave functions, open systems typically exhibit mixed states described by statistical ensembles of wave functions. To address the crucial stability issue, several recent studies have explored the persistence of topological order under decoherence [8, 9]. They have shown a connection between a phase transition in the mixed-state topological order and a breakdown of topological quantum memory—quantum information nonlocally encoded in topological order.
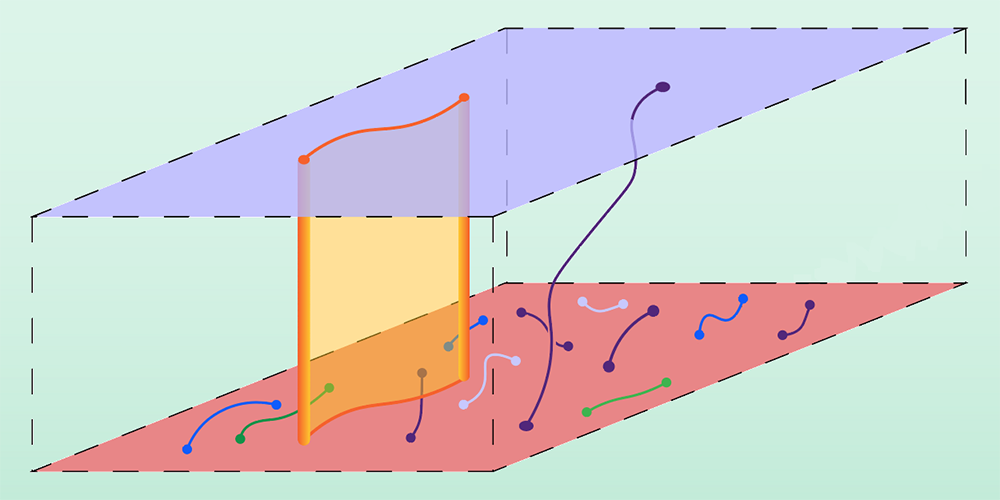
Dissipation and decoherence have been conventionally regarded as nuisances that obscure the observation of interesting physics, motivating efforts to suppress them in experimental setups and practical applications. However, as an alternative scenario, they may give rise to physical phenomena that have no counterparts in closed quantum systems. The three new theoretical studies [1–3] have explored this intriguing possibility, with the aim of revealing novel types of topological order that are possible only for mixed states of open quantum systems (Fig. 1).
Zijian Wang and colleagues at Tsinghua University in China [1] investigated a widely used model of topological order known as the toric code [5] under decoherence. They found that decoherence degrades topological quantum memory to classical memory, consistent with previous studies [8, 9]. Notably, they also revealed that careful application of decoherence can proliferate fermionic versions of anyons, whereas only bosonic versions are able to condense in pure states. The researchers determined that this mixed-state topological order retains long-range entanglement despite the loss of quantum memory—a phenomenon that has no analogs for pure states of closed quantum systems.
Ramanjit Sohal at the University of Chicago and Abhinav Prem at the Institute for Advanced Study in New Jersey [2] and Tyler Ellison and Meng Cheng at Yale University [3] developed a systematic understanding of intrinsic mixed-state topological order, laying the groundwork for comprehensive classification of its different forms. These two teams identified mixed-state topological order using so-called topological subsystem codes [10]. Such models can describe anomalous types of topological order, including premodular and chiral ones, which are widely deemed unattainable in the equilibrium ground states of closed quantum systems. The two teams’ findings suggest that engineered dissipation and decoherence can facilitate the realization of such anomalous topological order, demonstrating the rich many-body physics of open quantum systems.
Understanding diverse phases of matter and comprehensively classifying such phases are fundamental objectives in physics. The three new theoretical studies reveal that dissipation and decoherence can induce novel types of topological order rather than simply suppressing interesting quantum effects. Such topological order has no parallels in pure quantum states and is thus intrinsic to mixed states. Given that the toric code has been experimentally realized in engineered quantum devices, the intrinsic mixed-state topological order holds potential for practical applications in cutting-edge quantum information processing. The coming decades should see a wide variety of quantum phases unique to open quantum systems far from thermal equilibrium, inspiring further theoretical and experimental progress.
References
- Z. Wang et al., “Intrinsic mixed-state topological order,” PRX Quantum 6, 010314 (2025).
- R. Sohal and A. Prem, “Noisy approach to intrinsically mixed-state topological order,” PRX Quantum 6, 010313 (2025).
- T. D. Ellison and M. Cheng, “Toward a classification of mixed-state topological orders in two dimensions,” PRX Quantum 6, 010315 (2025).
- X.-G. Wen, “Colloquium: Zoo of quantum-topological phases of matter,” Rev. Mod. Phys. 89, 041004 (2017).
- A. Y. Kitaev, “Fault-tolerant quantum computation by anyons,” Ann. Phys. 303, 2 (2003).
- C. Nayak et al., “Non-Abelian anyons and topological quantum computation,” Rev. Mod. Phys. 80, 1083 (2008).
- K. J. Satzinger et al., “Realizing topologically ordered states on a quantum processor,” Science 374, 1237 (2021); G. Semeghini et al., “Probing topological spin liquids on a programmable quantum simulator,” 374, 1242 (2021).
- E. Dennis et al., “Topological quantum memory,” J. Math. Phys. 43, 4452 (2002).
- J. Y. Lee et al., “Quantum criticality under decoherence or weak measurement,” PRX Quantum 4, 030317 (2023); R. Fan et al., “Diagnostics of mixed-state topological order and breakdown of quantum memory,” 5, 020343 (2024).
- T. D. Ellison et al., “Pauli topological subsystem codes from Abelian anyon theories,” Quantum 7, 1137 (2023).