Ultracold Fermions Enter the Fractional Quantum Hall Arena
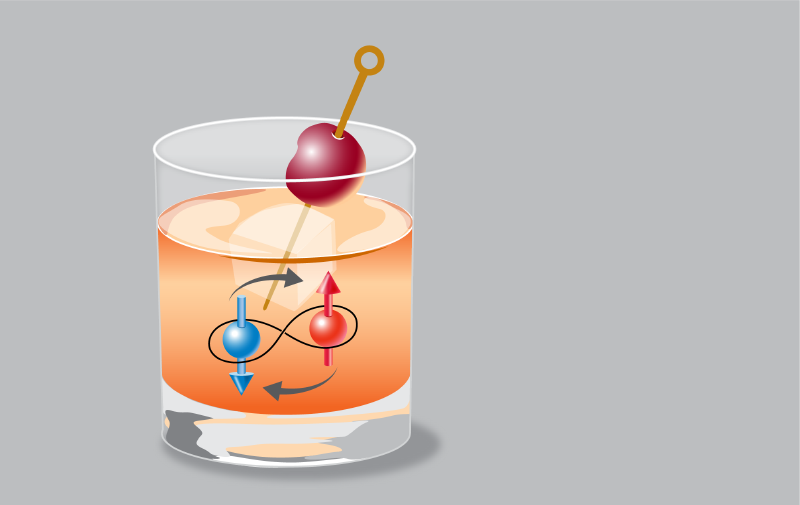
“More is different,” observed physicist Philip Anderson. He meant that the collective behavior of quantum many-body systems can produce entirely new physical effects, for example, the emergence of low-energy excitations carrying a fraction of the quantum of electric charge—the charge of an electron. To see this behavior happen at the most fundamental level of individual particles, scientists have built quantum simulators—machines that control individual atoms to mimic the properties of many-body ensembles of electrons. Now Philipp Lunt of Heidelberg University in Germany and his collaborators have gotten considerably closer to seeing how fractional charges emerge [1]. They emptied a metaphorical cocktail glass (an optical tweezer filled with ultracold fermions) to leave just one sip (a single pair of atoms). They stirred the remnants, mimicking the effect that a magnetic field has on real electrons, and thereby created something even more exciting: a cocktail of a strongly correlated atomic pair in a state whose wave function matches the one that physicist Robert Laughlin devised to describe the fractional quantum Hall effect. Besides being collective, the Laughlin state is also topological. The feat portends the use of cold atoms to dissect other, more exotic topological states, such as quantum Hall ferromagnets or topological p-wave superconductors.
The first Bose-Einstein condensates were formed in the mid 1990s. Soon after, quantum simulators explored relatively large ensembles using thousands of ultracold bosonic atoms. In such settings it’s possible to investigate the effects of an applied magnetic field by exploiting the equivalence of the Lorentz force experienced by charged particles and of the Coriolis force experienced by massive particles in a rotating reference frame. By stirring Bose-Einstein condensates [2, 3]—and shortly afterward, fermionic superfluids [4]—researchers were able to study the formation of vortex lattices similar to those observed in type-II superconductors subjected to a magnetic field. Increasing the rotation rate spawned more vortices. As a result, states resembling the fractional quantum Hall effect, in which the number of vortices exceeds the number of particles, seemed within reach. Unfortunately, dynamical instabilities and the large numbers of atoms in the clouds prevented early experiments from reaching that regime.
The astonishing degree of control over optical potentials has expanded the palette of parameters that can be adjusted and controlled, putting the goal of reaching the fractional quantum Hall regime and other topological states back on the cold-atom road map. By using high-resolution optical objectives, it was possible to image large rotating clouds of interacting bosons in situ and to prepare quantum states close to the fractional quantum Hall regime [5]. Alternative approaches using synthetic magnetic fields in optical lattices [6, 7] instead of rotating gases have also made considerable progress. The combination of the two techniques has led to the first realization of a diatomic bosonic Laughlin state [8]. In 2020, researchers realized a two-photon Laughlin state in a twisted cavity filled with Rydberg excitations that mediated strong photon–photon interactions [9]. The focus of all those experiments was on bosonic systems, not on electrons, which are fermions.
In their new experiment, Lunt and his collaborators began by trapping a handful of fermions (lithium-6 atoms) in tightly focused optical tweezers. With the help of a tilted potential, they tipped out most of the trapped atoms to leave exactly two fermions forming a spin singlet in the trap’s motional ground state. To approach the fractional quantum Hall regime, they spun up the fermions with a Laguerre-Gauss beam, whose structure carries orbital angular momentum. In the absence of interactions with each other, the two fermions would start to rotate individually inside the trap. However, to reach the fractional quantum Hall state, the fermions must not only interact, but they must also rotate around each other in a highly correlated fashion that embodies the state’s topological order.
Lunt and his collaborators solved this problem by tuning interactions between the spins using a Feshbach resonance. The state with all angular momentum carried by the center of mass of the pair experiences a shift of its energy because of the interactions between the constituent spins. However, the state where all angular momentum is transferred into the relative motion of the two particles has no contribution from the interaction energy. By avoiding being in the same place at once, the particles adopt the Laughlin state—more precisely, a Laughlin fractional quantum Hall state. Owing to the antisymmetry of the spin part of the wave function, the motional part of the wave function with two quanta of relative angular momentum represents a 1/2 Laughlin state.
To confirm that they had created a Laughlin state, the researchers varied the frequency of the Laguerre-Gauss beam and measured the resulting transfer rate out of the nonrotating initial state for various interaction strengths. They observed the expected independence of the Laughlin state’s energy on interaction strength. Using high-resolution in situ imaging and resolving each atom individually, they characterized the strong spatial correlations of the Laughlin state, conforming theoretical expectations with great accuracy.
A next goal will be the exploration of paradigmatic fermionic fractional quantum Hall liquids, such as the 1/3 Laughlin state formed by spin-polarized atoms. This goal should be within reach by utilizing p-wave Feshbach resonances and applying similar techniques to those pioneered by Lunt and his collaborators. However, sticking with fermions that possess spin is also exciting: In this case a rich phase diagram of various quantum Hall ferromagnets has been theoretically proposed [10], paving the way for an observation of magnetic skyrmions in ultracold atoms. These potential developments offer a complementary view on strongly correlated topological states of matter, which are drawing renewed attention in the condensed-matter community owing to their manifestations in two-dimensional van der Waals and Moiré materials.
References
- P. Lunt et al., “Realization of a Laughlin state of two rapidly rotating fermions,” Phys. Rev. Lett. 133, 253401 (2024); “Engineering single-atom angular momentum eigenstates in an optical tweezer,” Phys. Rev. A 110, 063315 (2024).
- J. R. Abo-Shaeer et al., “Observation of vortex lattices in Bose-Einstein condensates,” Science 292, 476 (2001).
- V. Schweikhard et al., “Rapidly rotating Bose-Einstein condensates in and near the lowest Landau level,” Phys. Rev. Lett. 92, 040404 (2004).
- M. W. Zwierlein et al., “Vortices and superfluidity in a strongly interacting Fermi gas,” Nature 435, 1047 (2005).
- M. Mukherjee et al., “Crystallization of bosonic quantum Hall states in a rotating quantum gas,” Nature 601, 58 (2022).
- M. Aidelsburger et al., “Realization of the Hofstadter Hamiltonian with ultracold atoms in optical lattices,” Phys. Rev. Lett. 111, 185301 (2013).
- H. Miyake et al., “Realizing the Harper Hamiltonian with laser-assisted tunneling in optical lattices,” Phys. Rev. Lett. 111, 185302 (2013).
- J. Léonard et al., “Realization of a fractional quantum Hall state with ultracold atoms,” Nature 619, 495 (2023).
- L. W. Clark et al., “Observation of Laughlin states made of light,” Nature 582, 41 (2020).
- L. Palm et al., “Skyrmion ground states of rapidly rotating few-fermion systems,” New J. Phys. 22, 083037 (2020).