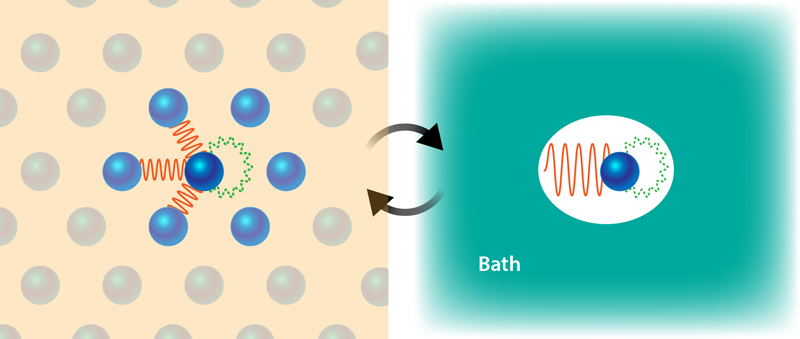
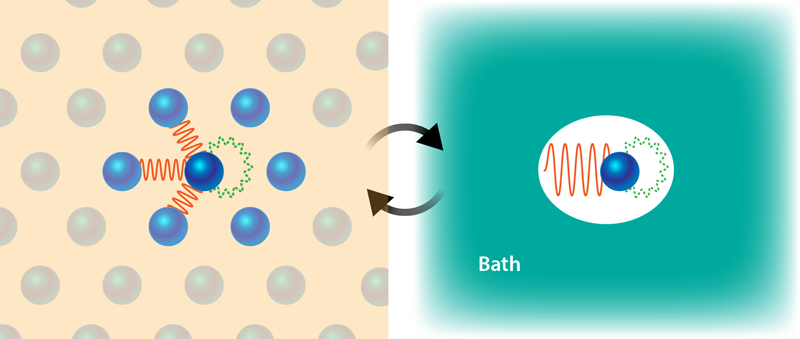
Embedding Correlated Electrons in a Multipurpose Bath
Searching for new types of superconductors, magnets, and other useful materials is a bit like weaving a tapestry with threads of many different colors. The weaver selects a short-range (local) pattern for how the individual threads intertwine and at the same time chooses colors that will give an overall (nonlocal) mood. A materials scientist works in a similar way, mixing atoms instead of threads, trying to match the motion of their electrons—their correlations—on both local and nonlocal scales. Doing so by trial-and-error synthesis is time intensive and costly, and therefore numerical simulations can be of huge help. To contribute to bridging computations to material discovery, Jiachen Li and Tianyu Zhu from Yale University have developed a new approach that treats local and nonlocal electronic correlations on an equal footing [1] (Fig. 1). They demonstrated their method by accurately predicting the photoemission spectra of several representative materials. Future work may lead to the identification and design of materials whose nonlocal effects can deliver desired electronic properties.
The door to modern computational prediction of material properties was arguably opened with the development of density-functional theory (DFT), particularly within the Kohn-Sham formulation [2]. Crucially, it introduced a rigorous approach to change a multielectron problem—consisting of, say, N electrons—into N separate one-electron calculations. DFT made possible the simulation of a wide array of solids and molecules in fields as disparate as biochemistry and planetary science. However, current implementations of DFT do not describe everything under the Sun. They can fail to capture the behavior of correlated matter, particularly so-called strongly correlated electrons, which are the driving force behind high-temperature superconductors, exotically behaving magnets, and many types of chemical catalysts. The dynamics of such electrons is dominated by competing energy scales, usually those associated with the kinetic energy and the electrostatic repulsion. Because of this competition, understanding the motion of any one electron seems to inevitably require following all the others as well—undercutting most popular implementations of Kohn-Sham DFT.
Enormous research efforts are ongoing to find accurate yet efficient descriptions of correlated electrons. Among these, a popular and successful family of frameworks follows the embedding strategy: Instead of decoupling all electrons into N one-electron problems, the idea is to simplify the system into a few-electron model embedded within a larger environment. Essentially, one divides the system into a fragment—a small number of electron orbitals identified as the main actors behind the electronic correlation—and a noninteracting bath representing the remaining orbitals. Upon self-consistently determining the bath parameters, this so-called impurity model offers an accurate description of local fragment correlations under the presence of the environment. The most famous member of this family of methods is probably the dynamical mean-field theory approximation [3], but several other schemes have had success [4–7].
While embedding frameworks have enabled significant contributions in the description of correlated solids and molecules, there is one key aspect that remains as an outstanding challenge: recovering the effect of electronic correlation beyond the embedded fragment. Indeed, the bath is typically built into embedding theories with little information about nonlocal interactions or with an insufficiently flexible structure to reproduce the effects of these interactions. An important frontier in current embedding research is thus involved with addressing this shortcoming [8]. The new strategy proposed by Li and Zhu is to add an effective interaction by systematically including nonlocal correlations in a multitier bath scheme.
The key to this development is combining ideas from various embedding techniques to capture nonlocal interactions with the full-cell embedding philosophy that Zhu has recently introduced [9]. The full-cell idea replaces the very small number of system orbitals within a traditional fragment by a small number of system atoms, each carrying up to hundreds of orbitals. This replacement results in a formidably complex impurity model that the researchers attacked with scalable quantum chemistry approximations. To add nonlocal correlation effects to these embedded atoms, Li and Zhu have now enhanced the structure of the bath. They allowed for interactions between bath orbitals, and they split these bath interactions into three distinct groups based on what they are meant to model: local charge distributions; local, low-energy charged excitations; and nonlocal correlations due to hybridization between the embedded atom and its environment. This layered approach allowed Li and Zhu to systematically recover nonlocal interaction effects without compromising the local description.
The researchers benchmarked this embedding method on a range of moderately correlated insulators, semiconductors, and metals, showing how it can predict aspects of the photoemission spectra of these materials in great agreement with experiment. Further, their formulation allows for analyzing the concrete contribution of nonlocal versus local correlations to the observables of interest. They used this interpretability to investigate an issue concerning descriptions of metallic sodium: DFT and other models predict a wider photoemission bandwidth than is observed experimentally, and improving such results is not straightforward. The researchers showed that this discrepancy comes from electronic correlations: Local atomic correlations constitute the main contribution, but nonlocal correlations are non-negligible up to fifth-nearest-neighbor effects.
The interacting-bath, full-cell embedding approach of Li and Zhu is an exciting addition to the embedding tool set, with the potential to bring the power of first-principles embedding to a new range of materials. Its fully systematic structure, capable of embedding full atoms and meaningfully reducing the choices necessary to include nonlocal correlations, hints at its promise for simulating challenging but technologically crucial material scenarios, such as material interfaces and rough surfaces. Furthermore, this method holds special promise for interpretative analysis of the nature of correlation effects in complex materials. Beyond the length-scale analysis exemplified in this first work, it will be interesting to see whether the classification of the bath into three physically distinct orbital types will allow for distinguishing different types of correlation effects in various materials. Such classification would contribute not only to explaining the extensive tapestry of correlated phenomena, but it would also help toward the design of materials and devices with targeted optoelectronic properties leveraging electronic correlation.
References
- J. Li and T. Zhu, “Interacting-bath dynamical embedding for capturing nonlocal electron correlation in solids,” Phys. Rev. Lett. 133, 216402 (2024).
- R. O. Jones, “Density functional theory: Its origins, rise to prominence, and future,” Rev. Mod. Phys. 87, 897 (2015).
- G. Kotliar et al., “Electronic structure calculations with dynamical mean-field theory,” Rev. Mod. Phys. 78, 865 (2006).
- S. Wouters et al., “A practical guide to density matrix embedding theory in quantum chemistry,” J. Chem. Theory Comput. 12, 2706 (2016).
- A. A. Rusakov et al., “Self-energy embedding theory (SEET) for periodic systems,” J. Chem. Theory Comput. 15, 229 (2018).
- P. V. Sriluckshmy et al., “Fully algebraic and self-consistent effective dynamics in a static quantum embedding,” Phys. Rev. B 103, 085131 (2021).
- C. Mejuto-Zaera, “Quantum embedding for molecules using auxiliary particles—The ghost Gutzwiller Ansatz,” Faraday Discuss. 254, 653 (2024).
- T. Maier et al., “Quantum cluster theories,” Rev. Mod. Phys. 77, 1027 (2005).
- T. Zhu and G. K.-L. Chan, “Ab initio full cell GW + DMF for correlated materials,” Phys. Rev. X 11, 021006 (2021).